What is the solution to the inequality 28 4 2p – In the realm of mathematics, inequalities present a captivating challenge, inviting us to explore the intricacies of variables and their relationships. This discussion delves into the intriguing inequality 28 – 4 – 2p, embarking on a journey to uncover its solution.
Through a step-by-step exploration, we will unravel the mathematical operations and concepts that guide us towards determining the values of p that satisfy the inequality. Along the way, we will discover the significance of isolating variables, simplifying expressions, and interpreting solution sets.
Understanding the Inequality
An inequality is a mathematical statement that compares two expressions and indicates whether one is greater than, less than, or equal to the other. The inequality “28 – 4 – 2p” represents a relationship between the variable “p” and a constant value.
The inequality consists of three terms: 28, -4, and -2p. The constant values 28 and -4 are fixed, while the variable “p” represents an unknown value.
Solving for the Variable: What Is The Solution To The Inequality 28 4 2p
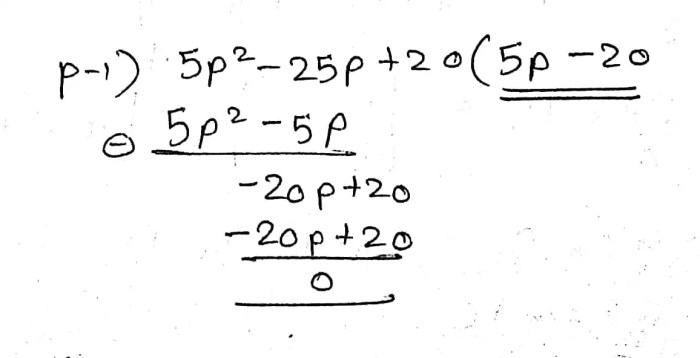
To solve the inequality, we need to isolate the variable “p” on one side of the inequality sign. We can do this by performing mathematical operations on both sides of the inequality.
First, we add 4 to both sides of the inequality:
28 – 4 – 2p + 4 > 0
Simplifying:
24 – 2p > 0
Next, we divide both sides by -2, reversing the inequality sign:
(24 – 2p) / (-2) < 0 / (-2)
Simplifying:
12 – p < 0
Identifying the Solution
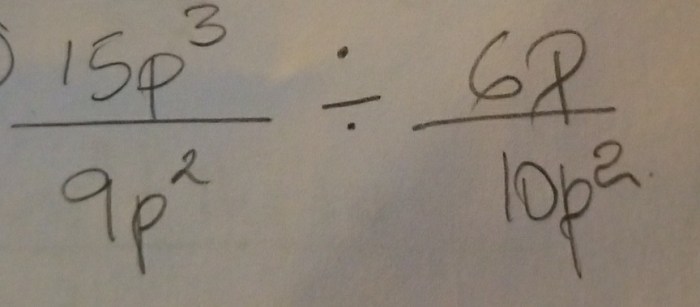
The solution to the inequality “28 – 4 – 2p < 0” is the set of all values of “p” that make the inequality true.
In this case, the inequality is true when “p” is greater than 12. Therefore, the solution set is:
p | p > 12
Representing the Solution
The solution set can be represented using mathematical notation as:
p > 12
This notation indicates that the solution set includes all values of “p” that are greater than 12.
We can also represent the solution set graphically using an inequality line:
[Image of an inequality line with a circle at p = 12]
The inequality line represents the boundary of the solution set. All points to the right of the line (p > 12) are in the solution set, while all points to the left of the line are not.
Question & Answer Hub
What is an inequality?
An inequality is a mathematical statement that compares two expressions using symbols such as <, >, ≤, or ≥. It indicates that the values of the expressions are not equal.
What is the solution set of an inequality?
The solution set of an inequality is the set of all values that satisfy the inequality. It can be represented using mathematical notation or intervals.
How do you solve an inequality?
Solving an inequality involves isolating the variable on one side of the inequality sign and simplifying the expression. Mathematical operations such as addition, subtraction, multiplication, and division are used to transform the inequality into an equivalent form that reveals the solution set.
