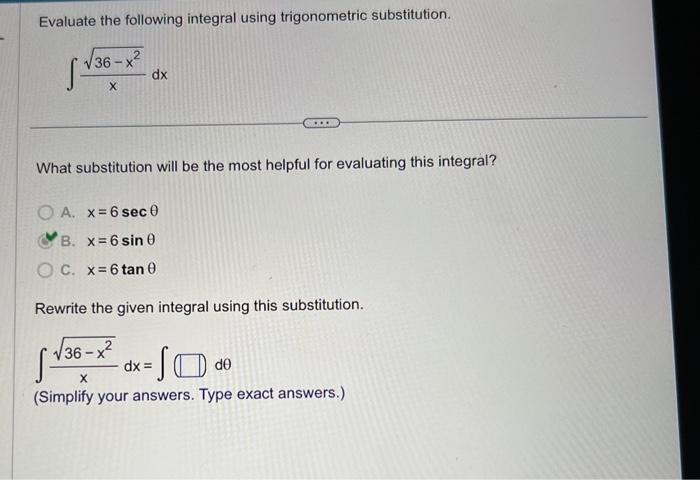
Evaluate the following integral using trigonometric substitution – In the realm of integral calculus, trigonometric substitution emerges as a powerful tool, enabling the evaluation of complex integrals with ease and elegance. This comprehensive guide delves into the intricacies of trigonometric substitution, empowering learners with a deep understanding of its methods, applications, and advanced techniques.
Through a step-by-step approach, we unravel the different types of trigonometric substitutions, showcasing their efficacy in solving a wide range of integrals. We explore the practical applications of trigonometric substitution in diverse fields, demonstrating its versatility as an indispensable tool in calculus, physics, and engineering.
Trigonometric Substitution: Evaluate The Following Integral Using Trigonometric Substitution
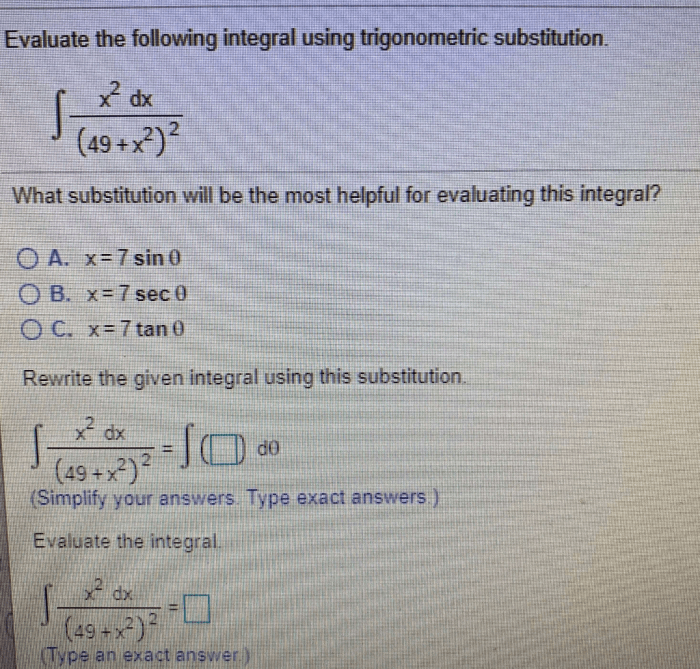
Trigonometric substitution is a technique used to evaluate integrals that involve algebraic expressions containing square roots of quadratic polynomials. It involves making a substitution that transforms the integrand into a trigonometric function, allowing us to use trigonometric identities to simplify the integral.
Methods of Trigonometric Substitution
There are three main types of trigonometric substitutions:
- Sine Substitution:Used when the integrand contains the expression \sqrta^2-x^2.
- Cosine Substitution:Used when the integrand contains the expression \sqrtx^2-a^2.
- Tangent Substitution:Used when the integrand contains the expression \sqrtx^2+a^2.
Examples of Trigonometric Substitution
Consider the integral \int \sqrt1-x^2 dx. Using sine substitution with x = \sin \theta, we get:
- dx = \cos \theta d\theta
- 1-x^2 = \cos^2 \theta
- \int \sqrt1-x^2 dx = \int \cos \theta \cos \theta d\theta = \int \cos^2 \theta d\theta
Applications of Trigonometric Substitution
Trigonometric substitution finds applications in various fields:
- Calculus:Evaluating integrals involving irrational expressions.
- Physics:Solving problems involving circular motion, pendulums, and other oscillatory systems.
- Engineering:Analyzing electrical circuits, mechanical vibrations, and fluid dynamics.
Advanced Techniques in Trigonometric Substitution, Evaluate the following integral using trigonometric substitution
Advanced techniques include:
- Integration by Parts:Used to integrate products of trigonometric functions.
- Integration by Partial Fractions:Used to integrate rational functions involving trigonometric functions.
- Complex Integration:Used to evaluate integrals involving trigonometric functions in the complex plane.
Resources for Learning Trigonometric Substitution
- Textbooks: Calculus by Stewart, Calculus by Thomas
- Online Tutorials: Khan Academy, Coursera
- Videos: YouTube, Brilliant
FAQs
What is trigonometric substitution?
Trigonometric substitution is a technique used to evaluate integrals by replacing the integrand with a trigonometric function and its derivative.
When should I use trigonometric substitution?
Trigonometric substitution is particularly useful when the integrand contains expressions like √(a² – x²), √(a² + x²), or √(x² – a²).
What are the different types of trigonometric substitutions?
The three main types of trigonometric substitutions are sine substitution, cosine substitution, and tangent substitution.